摘  要：卫星通信系统暴露在太空中，极其容易受到干扰，特别是当遇到跟踪干扰时，会严重影响跳频卫星通信系统性能。利用跳频信号与跟踪干扰信号之间的统计独立性，将跳频通信抗跟踪干扰问题转化为一个多数据集联合盲源分离（Joint Blind Source Separation，JBSS）问题，在独立向量分析（Independent Vector Analysis，IVA）的框架下进行干扰信号抑制。该方法同时利用了各信号之间的统计独立性和每个信号内部的统计相关性，有效提高了系统性能。仿真结果表明，所提方法在干扰压制比为 0.6 且信噪比为 15dB 的情况下，系统误码率相比基于能量相关性排序的独立成分分析（Independent Component Analysis，ICA）方法下降了 12.06dB，有效提高了卫星跳频通信系统抵抗跟踪干扰的能力。  

关键词：联合盲源分离；独立向量分析；跳频通信；跟踪干扰；通信抗干扰技术 

An Anti-Follower Jamming Joint Blind Source Separation Method for 

Frequency Hopping Communication System Based on IVA 

FENG Lu1，LI Changqing2*, LI Jiong2, LIU Yang1 

（1. Graduate School , Space Engineering University, Beijing 101400) 

（2. Space Information School, Space Engineering University, Beijing 101400) 

Abstract: Satellite communication system exposed in space is extremely vulnerable to interference, especially when it encounters follower jamming, which will seriously affect the performance of frequency hopping satellite communication system. Based on the statistical independence between frequency hopping signal and follower jamming signal, the anti-follower jamming problem of frequency hopping communication is transformed into a joint blind source separation problem of multiple datasets, and the follower jamming signal is suppressed under the framework of independent vector analysis. This method makes use of the statistical independence between signals and the statistical correlation within each signal, which effectively improves the system performance. The simulation results show that when the interference suppression ratio is 0.6 and the signal-to-noise ratio is 15dB, the bit error rate of the proposed method is reduced by 12.06dB compared with the independent component analysis method based on energy correlation permutation, which effectively improves the anti-follower jamming ability of satellite frequency hopping communication system. 

Key Words: joint blind source separation; independent vector analysis; frequency hopping communication; follower jamming; communication anti-jamming technology 

0 引  言 

    卫星通信技术凭借其通信距离远、覆盖面积大和通信线路稳定可靠等特点，已经成为现代生活中不可或缺的通信手段之一[1]。但由于卫星位置暴露在太空中，与地面的距离较远，很容易受到人为的干扰。为了抵抗人为干扰，大量的抗干扰技术已经被提出，其中跳频扩频（Frequency Hopping Spread Spectrum, FHSS）技术因其较强的抗干扰能力和良好的安全性已经广泛应用于卫星通信系统中[2]。跳频通信技术虽能高效应对各种阻塞式干扰，但对于跟踪干扰的应对能力有限[3]。为了限制跟踪干扰对跳频通信系统的损害，目前常见的方法有提高跳速[4]、改变跳频体制[5、6]、提高跳频组网能力[7]和利用干扰机的反应时间来传递消息[8、9] 等。这些措施主要采用“躲避式”的抗干扰方法，需要一定的先验知识，实现难度较大，且随着干扰设备水平的逐渐提升，可能会出现“避无可避”的情况，这些方法存在失效的风险。 

    盲源分离（Blind Source Separation，BSS）技术可以在源信号和传输信道参数未知的情况下，仅利用观测信号的时频特性、统计特性等特征，根据一定的准则恢复出各个源信号[10]。基于源信号与干扰信号的统计独立性，文献[11]利用独立成分分析（Independent Component Analysis，ICA）技术实现了跳频通信系统中窄带干扰信号的抑制。跟踪干扰信号是在跳频信号当前频率上发射的瞄准式干扰信号，可以将其看作频率不断跳变的窄带干扰信号。但如果将文献[11]的方法直接应用于跟踪干扰信号抑制中，会出现结果顺序不确定的问题，由此而引起的数据处理延时可能会引起数据存储灾难。文献[12]提出了一种利用信号的能量相关性进行信号排序较正的方法，但该方法的鲁棒性较差，仍未有效解决这一问题。

    跳频扩频卫星通信系统一般具有较宽的信道带宽，如美国的 AEHF 通信卫星跳频带宽可达1GHz 以上。在如此宽的频带上，各跳频频点的信道传输环境差异较大，因此跟踪干扰环境下的跳频通信系统是一种间歇式突变的混合系统。针对这一特点，本文将跳频通信抗跟踪干扰问题转化为多数据集联合盲源分离问题，提出了一种基于独立向量分析（Independent Vector Analysis，IVA）的跳频通信抗跟踪干扰方法。该方法巧妙地避免了 ICA 出现的排序问题，并且有效地提高了跳频通信“硬抗” 恶意跟踪干扰的能力。仿真结果证明了该方法的有效性。 

1 跟踪干扰 

    跟踪干扰机是一种具有侦测能力的干扰器，当其感知到其需要干扰的信号时立即发送干扰信号。在跳频通信系统中，跟踪干扰机可以在信号源发送跳频信号时对信号进行分析，并仅在目标信号的当前频率上发射干扰信号，而不需要预先知道跳频图案。跟踪干扰不仅极难预先检测，而且非常节能，对通信系统造成了严重威胁[13]。 

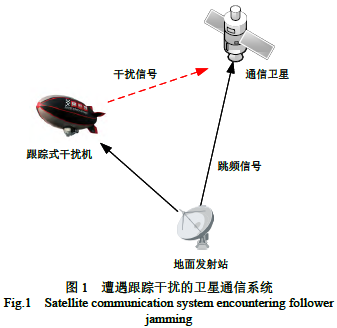
    图 1 描述了上行链路中遭遇跟踪干扰的卫星通信系统。地面发射站按照预定跳频图案向通信卫星发射跳频信号的同时，跟踪干扰机对侦测到的跳频信号进行分析，得到这一跳的发射频率，并在这一频率上向通信卫星发射跟踪干扰信号，影响通信卫星对信息的接收。

    一般来说，跟踪干扰机在感知到跳频信号后，需要一段时间的处理过程后才能发送干扰信号，而且由于传播路径不同，干扰信号存在传播时延。因此，在每个跳频周期中，跟踪干扰信号相对于跳频信号的起始点具有一定的延迟，并且该延迟在跳频周期内。如图 2 所示。 

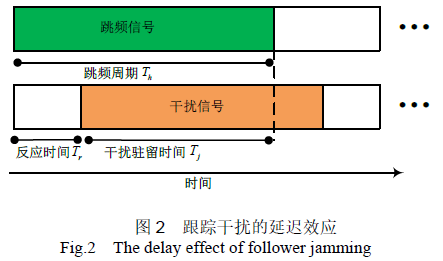
    将干扰信号的驻留时间j T 与跳频周期hT 的比值称为干扰压制比，表达式为：

    由于跟踪干扰在信号处理和传播距离上存在局限性，跟踪干扰机必须在特定的地理区域内工作，这种地域关系称为干扰椭圆[4]，即干扰机、发射机和接收机的配置距离必须满足以下公式：

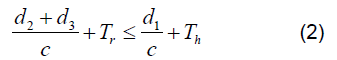
    式中， 1 d 、2 d 、3 d 分别为发射机与接收机的距离、干扰机与发射机的距离、干扰机与接收机的距离，c是光速（3108m/ s）， h T 是跳频周期， r T是干扰机所需的反应时间。将公式（2）经过变换可以得到：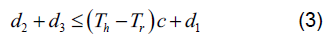

    将公式（3）的右侧可以看成常数，则构成了一个以发射机和接收机为2 个焦点的椭圆，干扰机必须在该椭圆上或在椭圆内部，当干扰机位于椭圆外时，干扰不再有效。在卫星跳频通信的跟踪干扰中，这种几何关系从二维空间上升为三维空间，干扰椭圆拓展为干扰椭球，如图3 所示。

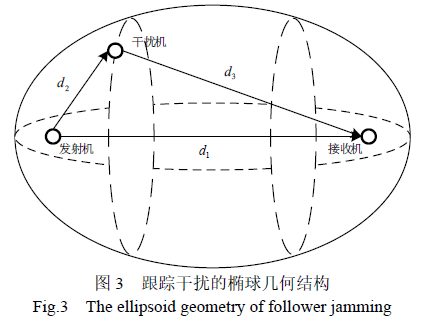
    对于上图所示的上行链路的跟踪干扰，干扰机越靠近发射机与接收机的连线，越可以快速准确地感知跳频频谱，并最大限度地缩短干扰机的响应时间，达到最佳干扰效果。由于跳频信号发射机与接收卫星的位置是固定和明确的，因此跟踪干扰可以极其方便地实现。

2 跳频通信抗跟踪干扰的联合盲源分离方法

2.1 系统模型

    卫星跳频通信系统由发射端、干扰机和接收端构成，系统模型如图4 所示。

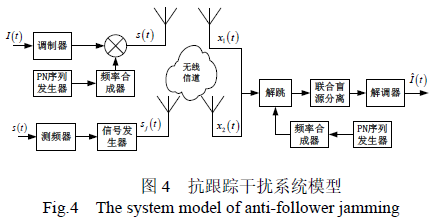
假设观察时间为 L ，共接受到的信号跳数为M ，则发送的跳频信号可以表示为：

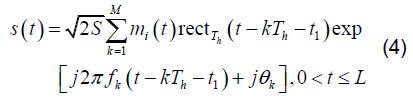
    其中， S 为信号功率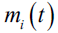，为经过基带调制的传输数据， k f 和k 为第k 跳的载波频率和相位，1t 为信号第一个跳变时刻，则第k 个跳变时刻为 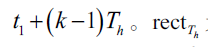为宽度为hT 的矩形窗，

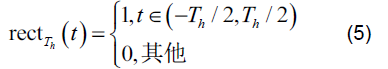
    跟踪干扰信号可以表示为：

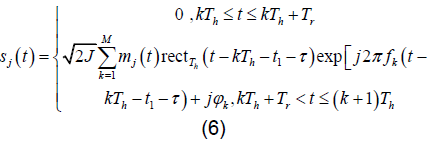
    其中， J 为干扰信号功率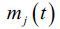，为跟踪干扰在基带调制的干扰信号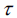，为干扰时延，由干扰机反应时延和信号传播时延两部分构成，表示为：

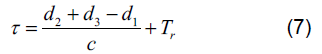
    在无线信道中，跳频信号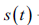与跟踪干扰信号混合在一起。图5 显示了跟踪干扰（黄色）对跳频信号（绿色）进行干扰的时频域表示。尽管跳频信号与干扰信号到达之间存在时间延迟，但信号受干扰情况仍然严重。

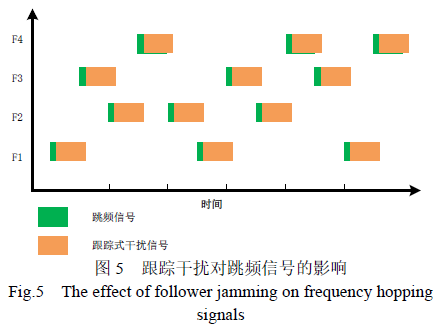
    注意到跟踪干扰信号与跳频信号形成的混合信号在时频域呈现出多段分布的特点，同时跟踪干扰信号与跳频信号来自不同发射机，满足统计独立的先决条件。因此，本文提出将跳频通信抗跟踪干扰问题转化为多数据集联合盲源分离问题，利用IVA 框架进行跟踪干扰抑制。

2.2 独立向量分析

    IVA 是最近兴起的一种多数据集联合盲源分离技术，可以看作是ICA 从单数据集到多数据集的扩展。IVA 将源信号建模为随机向量变量并同时处理，通过源信号向量之间的独立性将源信号分离，并通过源信号中各元素的相关性避免了各元素的排列问题。由于该模型包含了源信号各分量之间的依赖性，IVA 理论上不受顺序不确定性的影响，这是IVA在处理该问题的显著优势[14]。

    假设存在N 个接收天线，采集到K 个频点的数据（即K 个数据集），各数据集中每个信号存在L 个样本点，得到各频点信号的瞬时混合模型为：

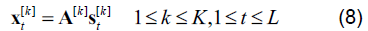
    其中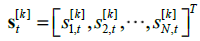，是零均值源信号矢量 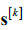的第t个样本值，上标T 为转置符号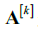， 是在第k 个数据集上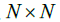的混合矩阵。第n 个源信号成分矢量（Source Component Vector，SCV）表述为 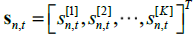，该 SCV中的元素独立于其他SCV 中的元素。此时，数据集中所有源信号的概率密度函数满足。

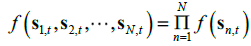    IVA 通过最小化估计的源向量之间的互信息量来识别SCV，目标函数表达式为：

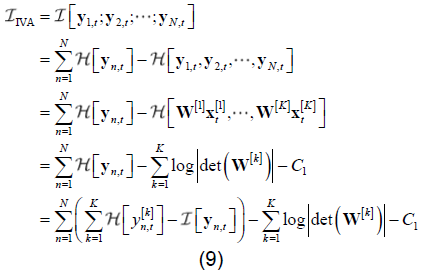
    其中， 表示SCV 中的互信息量， 表示估计源的信息熵， 1C 为常数项。通过最小化目标函数同时最小化了所有分量的熵，并且最大化了每个估计SCV 内的互信息，解决了跨多个数据集的排列歧义。通过 IVA，省去了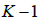次顺序调整的过程。对于目标函数的优化，可以通过自然梯度下降、牛顿拉夫森迭代[15]等方法来估计得到源信号。

2.3 基于IVA 的跳频通信抗跟踪干扰方法

    跳频信号在无线信道中遭遇跟踪干扰，混合信号被接收机的两根天线接收。首先，接收信号根据先验知识进行同步与解跳。如前所述，跟踪干扰信号相较于跳频信号存在一定的延时，而这保证了通信接收机能够实现跳频同步和解跳。

    然后，接收机存储多个跳频时隙、频段的数据，并按照跳频图案进行分段，将接收信号由单数据集构造为多数据集，

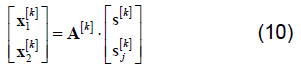
    其中，混合系数矩阵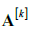的值取决于信道状态。跟踪干扰环境下的跳频通信系统是一种间歇式突变的混合系统，不同跳频频点的信道衰减系数不同。因此假设卫星通信信道是慢衰落信道，即信道衰减系数在不同跳频频点是变化的，但在某一跳频频点内信道状态是固定不变的。

    随后，利用IVA 框架对构造为多数据集的接收信号进行多数据集联合盲源分离，分解得到跳频信号与跟踪干扰信号在各频段上的估计信号

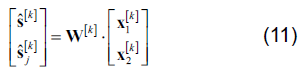
    其中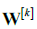， 为解混矩阵。对估计信号根据跳频图案进行重构，得到跳频信号的估计信号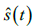与跟踪干扰信号的估计信号。

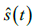    最后，对估计信号进行识别。跟踪干扰信号相较于跳频信号存在一定的时延，在干扰时延内，干扰信号幅值为0，而此时跳频信号幅值不为0。因此，跳频信号的估计信号与跟踪干扰信号的估计信号在时域波形上存在明显差异。通过设置一定阈值，对估计信号进行包络检测可以识别出跳频信号的估计信号 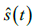。对其进行解调，便得到信息序列 。

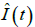    综上，该方法的信号处理流程框图如图6 所示。

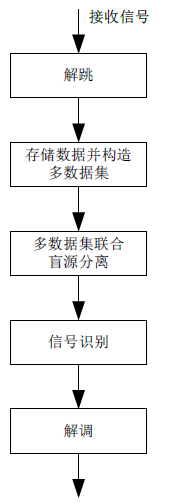
图 6 本文所提方法的信号处理流程框图

Fig.6 The signal processing flow chart of the method proposed in this paper

3 仿真性能分析

    本文通过模拟仿真来验证所提出的基于IVA 的跳频通信抗跟踪干扰方法。利用MATLAB 软件基于图4 通信系统搭建仿真平台。以AEHF 卫星通信系统为例，主要参数配置如表1 所示。

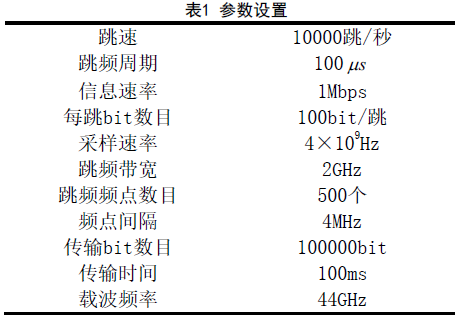
    为了仿真需求，本文假定跟踪干扰能够跟踪上跳频信号的概率为100%。跟踪干扰的干扰信号源采用随机数字码流[16]。为了更清晰地体现出本文所提方法的有效性和可靠性，首先对本文所提方法的迭代收敛情况进行了分析，随后将本文所提方法（IVA）、基于能量相关性排序的ICA 方法（E-ICA）[14]和未对信号处理等三种情况在不同干扰压制比和不同信噪比条件下的误码率进行了分析，最后分析了算法的计算复杂度。

3.1 迭代收敛情况

    本文采用性能指标（Performance Index，PI）[17]作为算法对源信号估计效果的评价标准，定义如下：

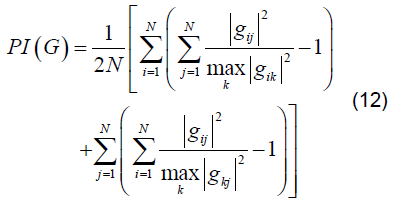
    其中，G 为全局传输矩阵且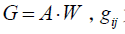 为G中第i 行第j 个元素。由定义可知，PI 值是一个不小于0 的数，当且仅当G 为广义排列矩阵时，即估计信号与源信号的波形完全相同时有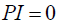。该指标越接近于0，则表明算法性能越好。本文所提方法的PI 收敛曲线如图7。

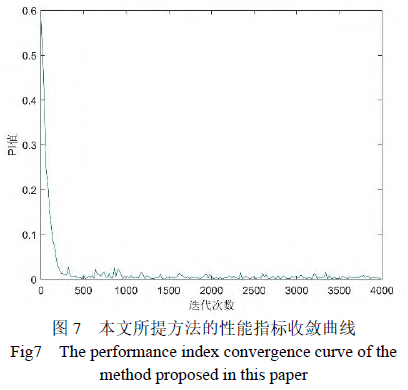
    从图中可以看出性能指标 PI 在大约500 步迭代时开始收敛达到稳定值，且算法的收敛点小于0.01，说明本文所提方法成功地估计出了跳频信号。

3.2 不同干扰压制比下的误码性能分析

    下面分析在不同干扰压制比下基于IVA 的跳频通信抗跟踪干扰方法对系统的性能影响。在信噪比一定的情况下，通过仿真对误码率进行计算。图8给出了在信噪比为15dB 的情况下，未处理干扰、基于E-ICA 的方法和本文所提出基于IVA 的方法的误码率曲线图。

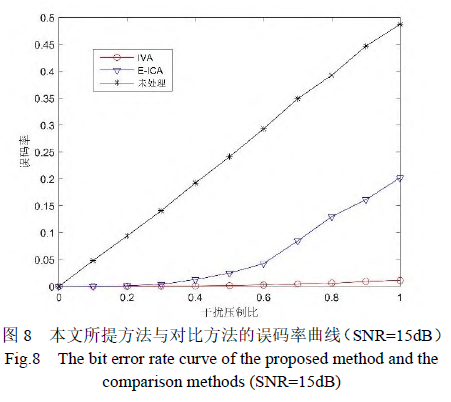
    从图 8 可以看出，在跟踪干扰压制比较小时，基于IVA 和基于E-ICA 的方法都可以取得较好的误码率，说明由于跟踪干扰存在的延迟效应，干扰只能够对每跳的后半段产生影响，干扰压制比越小对系统的影响就越小，两种方法抗干扰效果差距不大。当干扰压制比增大后，基于IVA 的方法的误码率上升速度始终小于基于E-ICA 的方法。这是由于基于E-ICA 的方法需要在干扰抑制后对源信号重新排序，系统性能下降，而IVA 通过目标函数的设计避免了这一情况。需要注意的是，干扰压制比为0 时，在实际情况中这代表着没有发生干扰。

3.3 不同信噪比下的误码性能分析

    下面分析在不同信噪比下，基于IVA 的跳频通信跟踪干扰抑制方法对系统的性能影响。在跟踪干扰压制比一定的情况下，通过仿真对误码率进行计算。图9 给出了在干扰压制比 为0.6 的情况下，未处理干扰、基于E-ICA 的方法和本文所提出基于IVA 的方法的误码率曲线图。

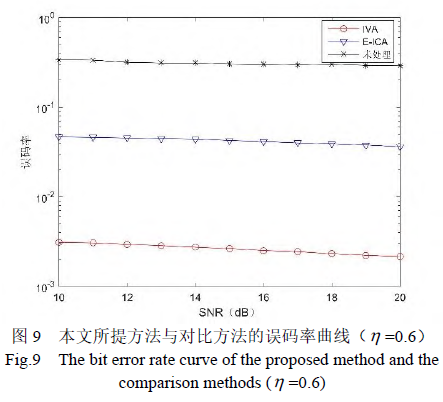
    从图 9 可以看出，干扰压制比一定的情况下，在未做任何处理时系统误码率变化幅度不大，系统误码率主要来自于跟踪干扰信号。当信噪比在10-20dB 区间时，本文所提出的基于IVA 的方法明显好于基于E-ICA 的方法。当SNR=15dB 时，基于IVA 的方法比基于E-ICA 的方法误码率下降了12.06dB。

3.4 计算复杂度

    本文所提出方法的计算复杂度主要体现在多数据集联合盲源分离算法中的计算迭代过程[18]。其中，协方差矩阵的计算复杂度为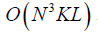 ，矩阵求逆的计算复杂度为 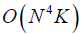。因此，每次迭代的计算复杂度可以表示为：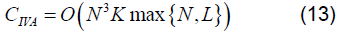

    可以看出，本文所提方法的计算复杂度主要与接受天线个数N 、频段个数K 、频段内采样点个数L有关。通信卫星的天线个数N 十分有限，因此算法的计算复杂度在可控范围之内，且随着高速信号处理芯片的发展，本文所提方法有着十分广阔的发展前景。

4 结束语

    针对跳频卫星通信系统遭遇跟踪干扰时系统性能下降的问题，本文利用跳频信号与跟踪干扰信号之间的统计独立性，将跳频通信抗跟踪干扰问题转化为一个多数据集联合盲源分离问题，在IVA 框架下进行干扰信号抑制。仿真结果表明，本文所提出的方法能够明显降低系统误码率，当干扰压制比为0.6 且信噪比为15dB 时，本文所提方法的误码率相较于基于E-ICA 的方法降低了12.06dB。本文的下一步工作是对IVA 算法进行针对性改进，使其更加适用于跳频卫星通信系统。