摘　要：目前所使用的窄带干扰抑制算法需要进行频谱复用，通信窄带受到不同干扰类型时，信号源发射功率大小难以调节，影响抑制算法的性能，本文提出一种基于傅里叶变换的跳频通信窄带干扰自适应抑制算法。获取跳频通信窄带信号发射机工作过程，对通信过程中的发射接收信号进行分析建模，得到信号发送和接收表示函数，设计自适应滤波器结构和内部转移函数，基于傅里叶变换计算信号最优阶次，识别干扰信号，通过削弱自适应的方式抑制跳频通信窄带干扰。算法性能分析结果表明：不同干扰类型下，设计干扰自适应抑制算法误码率和均方误差低于传统算法，且收敛速度更快。

关键词：傅里叶变换；跳频通信窄带；干扰抑制；自适应；算法设计

0　引言

现代通信技术的飞速发展，使得人们的生活变得更加丰富多彩，然而越来越多的电磁干扰也随之而来[1-2]。因此，对通信系统而言，最大限度地降低干扰成为一项重要工作。跳频通信作为一种无源通信方式，以其灵活的频率选择、短距离高速传输等优点被广泛应用于现代通信领域。但是由于信号在到达目标前会受到大量的窄带干扰和频率选择性衰落等因素影响致使系统性能严重下降，因此，自适应信号处理技术是提高跳频通信抗干扰能力、改善系统性能的关键技术之一[3-4]。目前所使用的窄带干扰自适应抑制算法主要分为两类：线性自适应性干扰抑制算法和基于功率谱密度估计的自适应性干扰抑制算法。线性自适应性干扰抑制技术利用了传统算法中对最大似然估计误差的容忍能力较强这一优点；而基于功率谱密度估计的自适应干扰抑制理论则是基于对信号频谱特性及统计特性进行估计而达到抑制效果最好且算法复杂度较低的一种方法[5-6]。通信跳频信号在实际的使用过程中，所产生的窄带干扰严重影响了跳频通信系统的性能。上述的两种窄带干扰抑制算法需要进行频谱复用，在不同干扰类型下，对于信号源发射功率大小难以调节，影响抑制算法的性能。本文提出了一种基于傅里叶变换的跳频通信窄带干扰自适应抑制算法，提升跳频通信窄带干扰的抑制效果。

1　跳频通信窄带干扰自适应抑制算法设计

1.1　建立跳频通信窄带信号模型

跳频通信窄带干扰抑制技术是变换域干扰抑制技术当前的热点研究方向，跳频通信系统是在一个频率为一条窄带（或称频带）内，利用特殊的跳频调制技术，由载波信号和调制信号产生[7-8]。当跳变周期等于某一特定频段内其他用户信道的周期时，通信双方能够在该信道中进行数据传输。在设计跳频通信窄带干扰自适应抑制算法前，需要对通信过程中的发射接收信号进行分析建模。信号发射机示意图如图1所示。

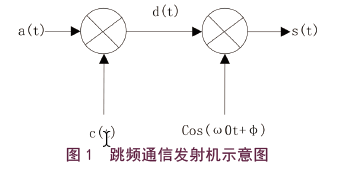
图1中，a（t）为通信系统中的基带信息，c（t）为伪随机码，d（t）为直跳信号，s（t）为经过调制之后的带通发送信号。当用户按给定的速率和跳频周期进行数据传输时，通信双方将获得跳频信号[ 9 ]。因此，我们可以将跳频通信看作是一个窄带的载波信号。基带信息可以表示为：

式中，a,为以概率为分布标准的分段函数，g。表示基带的形成函数，T,表示接收信号在时间域内的频谱，利用调制载波来发送信号，其形式可以表示为:

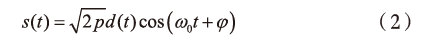
其中，p为信号发射功率，cos(ω。t+p)表示接收信号在频率域内的频谱，q表示接收信号的采样频率，ω。表示接收信号的时延偏差，t表明检测的时间范围「10-12。在不考虑失真的情况下，在对接收信号进行滤波处理后，如果在该信号中存在窄带干扰，则需要对接收信号的频谱进行检测和估计。接收信号表示为:

n(t)和j(t)分别表示信号传输过程中的白噪声和干扰，这两者都是预期内信号，可以进行正常解调。至此，完成跳频通信窄带信号模型的建立。

1.2　设计自适应滤波器

为了保证信号的分析效果，需要接触滤波器阈值的限制。在原有的干扰抑制算法中，其中的非线性自适应滤波器中的延迟单元在处理多重干扰的过程中，会出现记忆深度不足的情况。本文设计的自适应滤波器结构如图2所示。

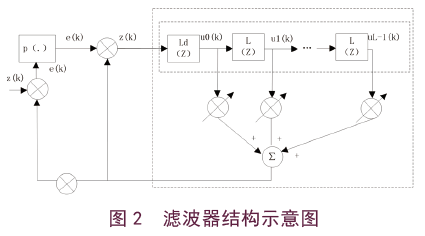
在图2中，p（.）表示非线性的结构处理单元，大虚线框中的部分能够实现窄带干扰预测，中间的虚线框中为一个延迟节点。本文的自适应滤波器在设计过程中的原则是，在满足滤波精度和计算复杂度前提下，尽可能地降低计算量[13-15]。为了使其能有效抑制窄带干扰，需要将接收信号做傅里叶变换到时域上，此时需要对每个频点进行傅里叶变换，形成相应的时域信号，此时，滤波器在参数选择上需要进行计算。对于跳频通信系统来说，所接收到的每一个信号都需要进行处理，这就要求对其进行复杂度分析。其延迟节点的网络中具有应急响应特征，其转移函数表示为：

式中， a表示采样周期T的频率分量的均值，即采样频率，其取值范围在0～1， z表示一个时域信号在时域上是连续分布的。延迟节点中的抽头输出处的转移函数表示为：

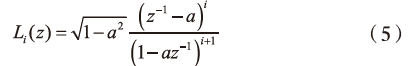
从上式中可以看出，采样频率稳定在标准范围内，本文所设计的自适应滤波器可以对通信跳频信号进行窄带干扰抑制，滤波器能够稳定运行。在参数调节的过程中，滤波器的记忆深度会发生变化，此时会脱离滤波器阶数的控制，增强滤波效果。根据上面设计的滤波器转移函数可知，该滤波器输出为一个窄带干扰检测结果，而不是检测到干扰所需要的采样频率和时延偏差等信息。

1.3　基于傅里叶变换的抑制算法优化

在系统中，通常情况下，干扰信号的幅值和频率是不确定的。当干扰信号到达接收机后，会受到一些因素影响而改变其频谱特征。如果不能通过对干扰信号的频谱进行分析得出结论，就会对后续的通信产生不利影响。本文采用傅里叶变换来优化干扰自适应抑制的算法复杂度，傅里叶变换能够将跳频通信窄带进行分解和化简。对于跳频通信窄带的数字序列x(n)来说，其中的正变化定义为：

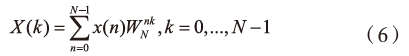
其中，N为采样点总数，n表示信噪比，W表示频谱功率谱，k表示干扰信号的相位。跳频通信窄带中每次采样都需要进行N次的复数乘法和复数加法，W、则具有一定的周期性。在实际应用中，如果需要进行干扰抑制，那么则需要进行运算量的递减。根据不描述系数的特点，进行河滨运算，将长的数据序列进行变换，将跳频通信窄带的数字序列x(n)按照n的取值不同划分为两组:

上式中， n按照奇偶性进行划分，需要保证信噪比和频谱功率之间具有一定的相关性；如果满足r=0，则可以对窄带干扰信号进行抑制。在以上计算下，离散傅里叶变换的频谱是一个多项式。对于接收信号，其频谱经过自适应滤波器后，频谱可以看成最优阶次的特殊长记忆信号，利用时间域和频率域进行滤波操作，得到傅里叶变换过程中的最优阶次，并将其作为干扰抑制的判决依据。在通信窄带中，载波为正弦波，其幅值和相位是恒定的。跳变周期由载波频率决定其变化规律，假设载波频率和跳变周期已知，那么则可以得到跳变点所对应的频点。而这些周期在不同的时刻对应不同的跳变周期。因此，可以利用这些周期值将载波频率转换为相应时间间隔内对应的载波频率值。根据本文所提出的窄带干扰的概念和特性，可以把接收到的调制信号转化为载波调制下的窄带干扰信号模型。为了获得可靠的通信信号传输，在时域上要满足一定性能指标要求（如符号同步、误码率等）。在抑制算法中，计算各阶次的分数傅里叶变换值，通过峰值大小确定不同类型下的干扰对应的最优分数傅里叶变换阶次，再通过阶次值判定干扰的类型，通过对峰值对应的FrFT域频率陷波来抑制跳频通信窄带干扰。在整体的算法流程中，首先对跳频通信窄带信号进行汉明窗加窗处理，由于傅里叶变换自身具有一定的周期性，为了保证加窗处理的有效性，考虑到傅里叶变换的周期性，以某一间隔建立一个周期内的阶次序列数组，计算该数字中不同阶次对应的信号变换，并搜索每次经过变换之后的傅里叶峰值，能够得到峰值序列。比较峰值序列中的各相元素，能够求得极值和对应的阶次。此时判断该阶次是否为1，如果为非1阶次，那么能判定为长时间记忆干扰，此时需要对该值进行削弱。经过削弱之后，傅里叶变换频谱的逆变换可以通过计算得到，此时能够获取时域信号。按照以上的流程进行计算，直到极值对应的阶次为1，此时完成跳频通信窄带的所有干扰抑制。至此，完成基于傅里叶变换的跳频通信窄带干扰自适应抑制算法的设计。

2　算法性能验证

2.1　实验设计

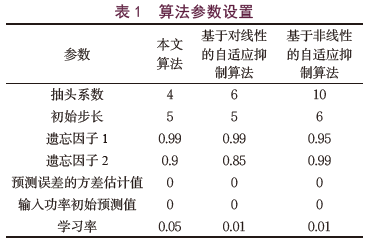
为了实现对本文设计的基于傅里叶变换的跳频通信窄带干扰自适应抑制算法有效性的证明，在算法性能验证中，选择基于对线性的自适应抑制算法和基于非线性的自适应抑制算法作为对照组，利用误码率和均方误差这两个指标对跳频通信窄带干扰自适应抑制算法的优劣进行评判。在实验中，需要设计跳频通信窄带的相关参数。其中，令背景噪声的方差数值为固定值，表示为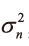，其数值恒定为0.01，跳频通信信号的幅度大小可以通过BPSK进行调制，跳频码的长度为29，采样频率为13kHz，采样点数为6300个，蒙特卡罗仿真次数为100次。实验中，需要在以上信号中人为加入干扰。在实验中，主要考虑单音干扰和AR窄带干扰两种类型。单音干扰的频率为1.5kHz，此时AR窄带干扰主要是通过二阶滤波器获取，滤波器两端点的z值为0.99，此时的AR窄带干扰信号可以表示为：

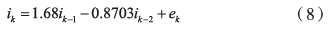
上式中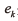， 表示白噪声干扰振幅。根据不同算法的最优参数，在实验中对算法参数进行设置，具体如表1所示。

在以上的实验环境下，计算不同算法下的误码率和均方误差。其中误码率的计算公式如下式所示：

上式中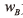， 为抑制过程中错误的信号数据比特数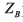， 为总的传输比特数；均方误差的计算公式为：

其中， N表示独立的实验次数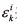， 表示第i次独立实验中算法经过k次更新之后，干扰自适应抑制算法的预测误差值。为了保证数据的准确性，需要尽可能地增加独立实验次数。在以上的实验下，分析不同算法下的测试结果，进行对比与分析。

2.2　实验结果对比与分析

在以上的实验流程下，得到不同算法在单音干扰形式下的误码率。

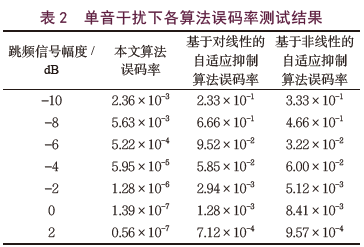
从表2中可以看出，在单音干扰的条件下，本文设计的算法误码率在不同的跳频信号幅度下，数值相比两种传统的干扰抑制算法更小。在AR干扰下，各算法的误码率测试结果如表3所示。

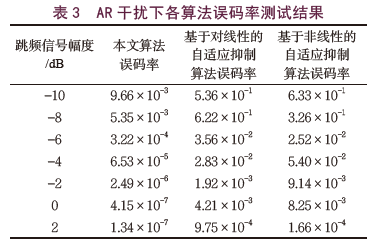
根据以上两个表的数据可以看出，无论接收信号中存在什么类型的干扰，本文设计的自适应抑制算法的误码率都更低，说明本文算法的抑制效果更好。在以上实验测试环境下，均方误差性能测试中，设定跳频信号幅度为0dB固定不变，对AR干扰的抑制效果进行观察，得到的各个算法的均方误差性能测试结果如表4所示。

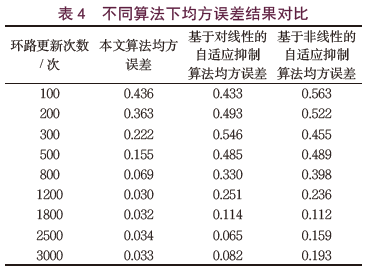
从表4中可以看出，本文设计的抑制算法在环路更新次数为1200次的时候，误差相对稳定，说明本文算法的收敛速度更快，两种传统算法不仅收敛速度慢，且均方误差也大于本文算法。

综上所述，本文设计的基于傅里叶变化的跳频通信窄带干扰自适应抑制算法在不同的干扰类型下，其性能均优于两种传统算法，不仅误码率和均方误差低于传统算法，且收敛速度更快。

3　结语

本文针对跳频通信系统中的窄带多类型干扰抑制问题提出了一种新的基于傅里叶变换的跳频通信窄带干扰自适应抑制算法。本文算法通过深入研究跳频通信窄带信号，设计了滤波器结构，并利用傅里叶变换识别信号干扰，并进行抑制。本文设计的算法能够避免阈值影响，省略频谱复用，精准控制信号源发射功率大小，保证干扰抑制效果，且具有一定的普适性。

王旭 阜阳职业技术学校，安徽阜阳，236000

参考文献

[1] 高东生,廖泓舟,王侃,等.一种适用于椒盐-高斯干扰信号的自适应滤波改进算法[J].电讯技术,2021,61(12):1554-1561.

[2] 孙沙沙,王鹏.自适应短波通信系统跳频信号时差定位方法[J].计算机仿真,2021,38(01):162-166.

[3] 江友华,朱毅轩,江相伟,等.基于改进LMS自适应滤波的局部放电噪声抑制方法[J].科学技术与工程,2022,22(03):1039-1047.

[4] 张亮,张翔宇,杨大伟,等.基于2D-RFRFT的密集假目标干扰自适应抑制算法[J].电光与控制,2022,29(03):53-58+64.

[5] 宋立业,蒲霄祥,李希桐.基于广义S变换和随机子空间的局放窄带干扰抑制方法[J].电工电能新技术,2021,40(11):29-36.

[6] 张晓璐,全厚德,孙慧贤,等.对偶序列跳频通信系统的等待匹配式自同步捕获方法[J].探测与控制学报,2021,43(01):88-94.

[7] 李向群,伍亚萍,庄旭菲,等.结合广义S变换和快速独立分量分析的局放信号中窄带干扰抑制方法[J].现代电力,2022,39(05):597-604.

[8] 饶显杰,周凯,汪先进,等.基于改进SVD算法的局部放电窄带干扰抑制方法[J].高电压技术,2021,47(02):705-713.

[9] 傅东宁,廖桂生,黄岩,等.基于图拉普拉斯嵌入的合成孔径雷达时变窄带干扰抑制算法[J].系统工程与电子技术,2022,44(06):1846-1853.

[10] 赵知劲,朱家晟,叶学义,等.基于多智能体模糊深度强化学习的跳频组网智能抗干扰决策算法[J].电子与信息学报,2022,44(08):2814-2823.

[11] 康雅洁,林艳,张一晋.基于贝叶斯学习的无人机集群抗干扰智能快跳频算法[J].航天控制,2022,40(02):73-78.

[12] 陈静,任婵婵,刘金山,等.一种导航信号频域干扰抑制方法及其FPGA实现[J].电讯技术,2022,62(05):585-590.

[13] 邵晓浪,胡泰洋,肖泽龙,等.基于LTE信号外辐射源雷达的同频干扰抑制算法[J].兵工学报,2021,42(08):1670-1679.

[14] 苏国瑞,林浩坤,蒲涛,等.抑制多用户干扰的串行反馈干扰抑制算法研究[J].量子电子学报,2021,38(06):880-888.

[15] 李冬霞,王雪,刘海涛,等.基于EBSBL-BO算法的L-DACS系统干扰抑制方法[J].信号处理,2022,38(10):2192-2200.

更多分享请继续关注logicRF官网www.logictile.com